Les internautes sont déconcertés par un problème mathématique de niveau collège.
Les enigmes mathématiques sont fascinantes. Elles ont le pouvoir de stimuler notre esprit et de défier nos compétences en résolution de problèmes.
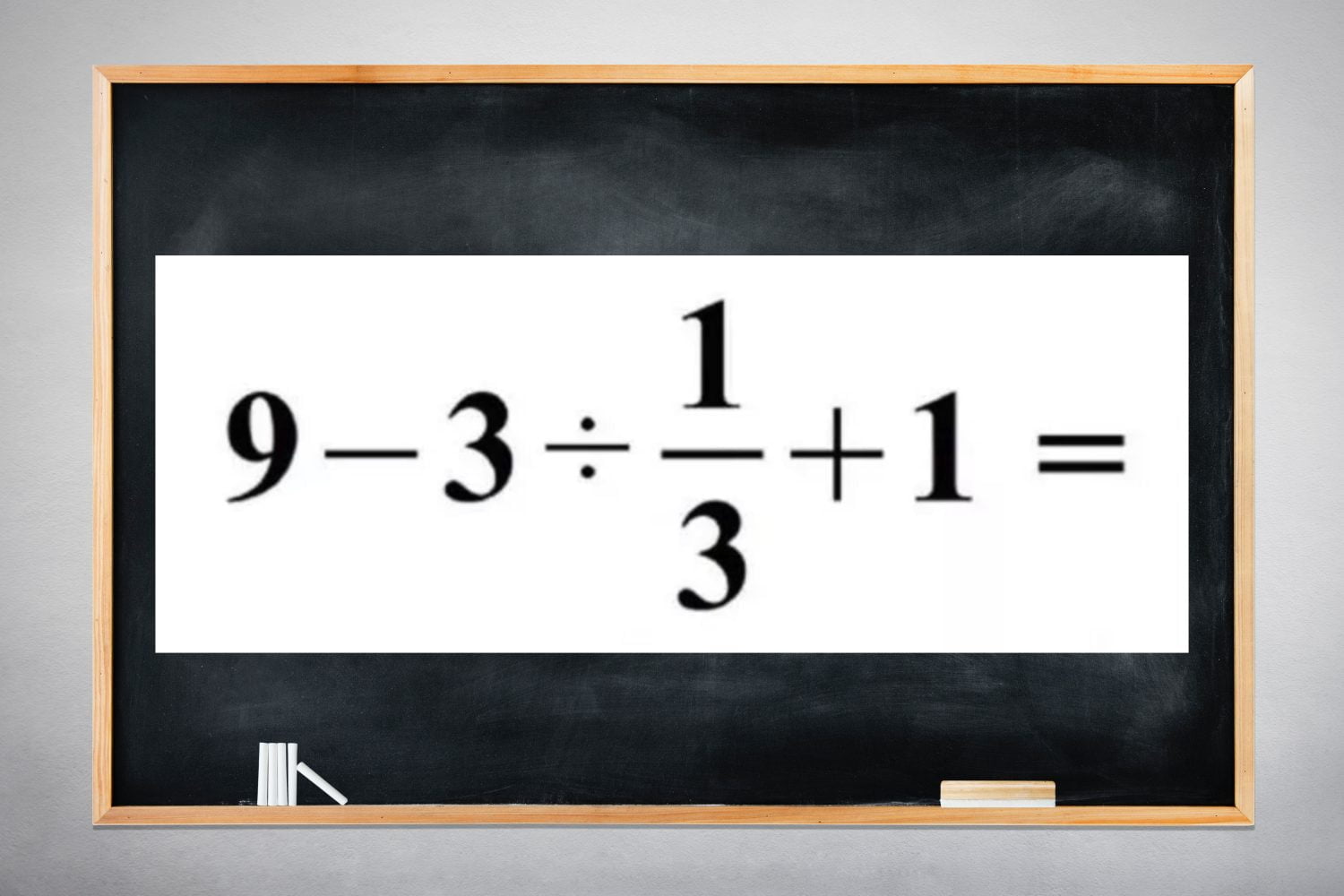
Il n’est pas rare de voir certaines enigmes devenir virales, attirant l’attention de nombreuses personnes, tant pour leur simplicité apparente que pour leur complexité sous-jacente.
L’attrait des enigmes mathématiques
Les enigmes mathématiques ont un attrait universel. Elles nous poussent à réfléchir de manière créative et à trouver des solutions intelligentes aux problèmes posés. C’est pourquoi elles sont souvent partagées et discutées en ligne, devenant ainsi virales.
Un exemple récent est une enigme mathématique de niveau collège qui a déconcerté de nombreux internautes âgés de 20 à 30 ans. Cette énigme, qui impliquait une combinaison d’opérations arithmétiques simples, a donné du fil à retordre aux internautes. Pourtant, en suivant les règles de base des mathématiques, la réponse n’était pas si difficile à trouver. Le secret pour résoudre cette énigme résidait dans l’identification des priorités opératoires et la compréhension des règles de base en mathématiques.
L’importance de l’analyse et de la déduction
Les enigmes mathématiques mettent souvent l’accent sur notre capacité à analyser et à déduire des informations, plutôt que sur nos connaissances mathématiques pures. Ces compétences sont essentielles pour résoudre des problèmes complexes et sont également évaluées lors de tests de QI.
Un exemple de ce type d’énigme est une séquence de chiffres avec un point d’interrogation qui représente un chiffre manquant. Pour résoudre cette énigme, il est nécessaire de faire preuve de logique et d’analyse, en examinant attentivement la séquence et en cherchant des motifs ou des relations entre les chiffres.
Les compétences mathématiques et la personnalité
Les enigmes mathématiques peuvent également nous en apprendre davantage sur notre personnalité et la façon dont les autres nous perçoivent. En comprenant comment nous abordons et résolvons les problèmes, nous pouvons mieux comprendre nos forces et nos faiblesses, ainsi que notre façon d’interagir avec les autres.
Il est intéressant de noter que les compétences en mathématiques ont été étudiées par la science. Des chercheurs se sont demandé si les professeurs de mathématiques et les génies de l’arithmétique pourraient avoir un avantage biologique. Une étude a cherché à déterminer si les compétences mathématiques d’une personne étaient associées aux concentrations de deux neurotransmetteurs clés impliqués dans l’apprentissage : le GABA et le glutamate.
Des chercheurs en neurosciences cognitives de l’Université d’Oxford au Royaume-Uni ont examiné les niveaux de GABA et de glutamate dans le cerveau pour voir si ces neurotransmetteurs pouvaient prédire les compétences mathématiques futures. Le GABA et le glutamate sont deux acides aminés naturels qui jouent des rôles complémentaires : le premier inhibe ou réduit l’activité des neurones dans le cerveau, tandis que le second les rend plus actifs. Leurs niveaux fluctuent tout au long de la vie.
Les chercheurs ont non seulement trouvé un lien entre les compétences mathématiques et les niveaux de neurotransmetteurs, mais ils ont également constaté que ces niveaux changeaient à mesure que les enfants grandissaient et devenaient adultes. Ces recherches ont été publiées dans la revue PLOS Biology.
Voici La réponse
En premier lieu, il est essentiel d’adopter une approche pragmatique et d’identifier les opérations prioritaires. En ce qui concerne le programme de mathématiques de quatrième, la multiplication et la division doivent être effectuées avant l’addition et la soustraction. Par conséquent, il n’est pas approprié de calculer les additions et soustractions de manière linéaire, comme par exemple en effectuant d’abord 9 – 3, puis 6 – (1/3) et ensuite 18 + 1, car cela conduirait à des résultats erronés, comme c’est le cas pour la plupart des internautes.
Cependant, il reste la question de la fraction. Comment procéder à sa division ? En réalité, il faut utiliser une méthode appelée « multiplication inverse ». Ainsi, il faut multiplier le numérateur par le dénominateur qui est également égal à 3. Donc, l’expression devient (9 – 3×3 + 1). Par la suite, il suffit de multiplier les numérateurs et les dénominateurs entre eux afin de simplifier la fraction. Ainsi, (3×3/1) équivaut à 9. Il ne reste plus qu’à calculer le tout : 9 – 9 + 1 = 1. Et voilà, le tour est joué.